Research

My research builds mathematical and computational bridges between theory and real-world decision-making.
I work at the intersection of applied category theory, Bayesian machine learning, and dynamic system modeling, developing composable and data-informed approaches to understand complex adaptive systems—especially in public health and epidemiology.
The ultimate goal is to create modeling tools that are modular, interpretable, and useful for guiding policy and intervention.

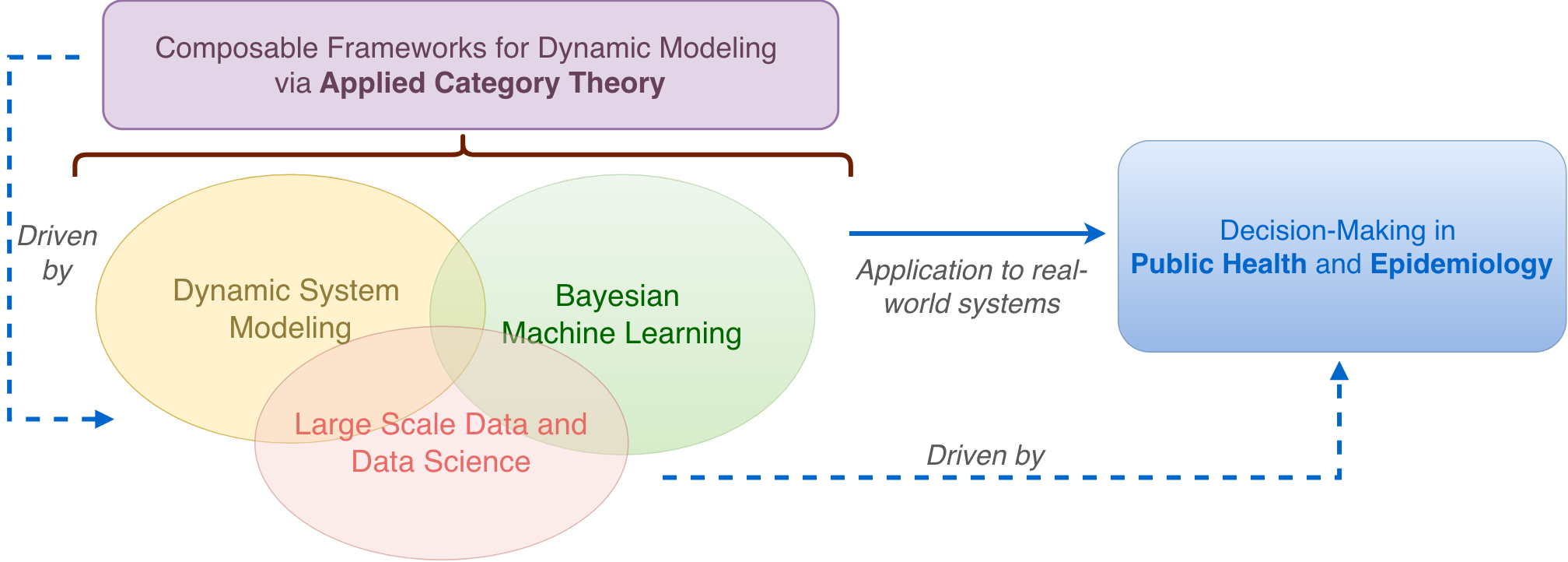
Conceptual overview of my research program.

Research Interests

My program integrates mathematical theory, software infrastructure, and data-driven modeling to advance compositional and interpretable frameworks for dynamic systems.
It consists of two deeply interconnected lines—one theory-driven, rooted in category theory, and one application-driven, motivated by urgent societal challenges.

1️⃣ 🧩 Theory-Driven Line — Category Theory for Next-Generation Dynamic System Modeling

We ask how mathematics can serve as a language for modeling change, and how it can reveal the hidden structures of dynamic models. This line reconstructs the mathematical foundations of dynamic modeling using applied category theory and translates these insights into open-source computational tools that make model composition transparent and rigorous.

a. Theoretical frameworks

We apply category-theoretic methodologies to a range of dynamic modeling paradigms—including
System Dynamics (SD), Agent-Based Modeling (ABM), Discrete-Event Simulation (DES), and Bayesian machine learning–based data-driven dynamic models — to construct modular, composable, and structure-preserving frameworks for next-generation dynamic modeling.

This theoretical groundwork enables interoperability and structure-preserving transformations across paradigms, paving the way for a new generation of modular, mathematically sound modeling environments.

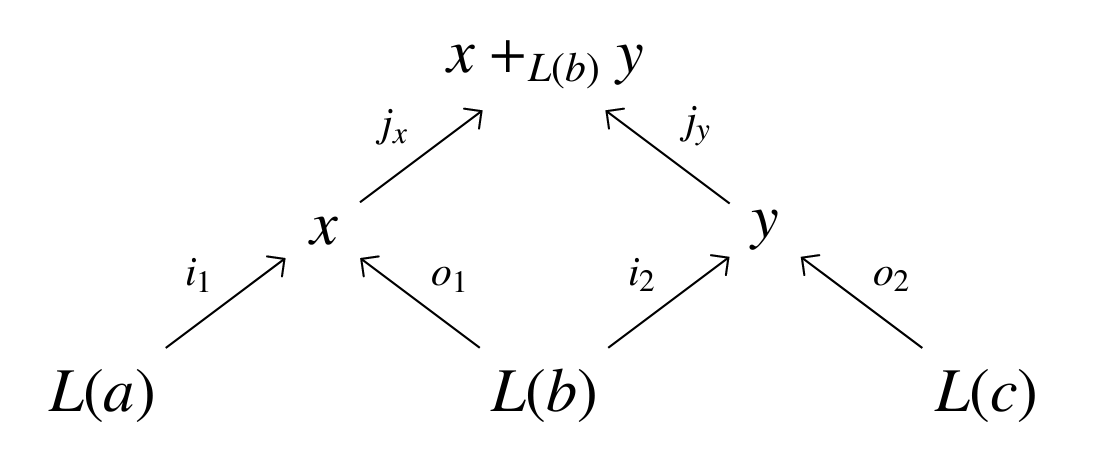
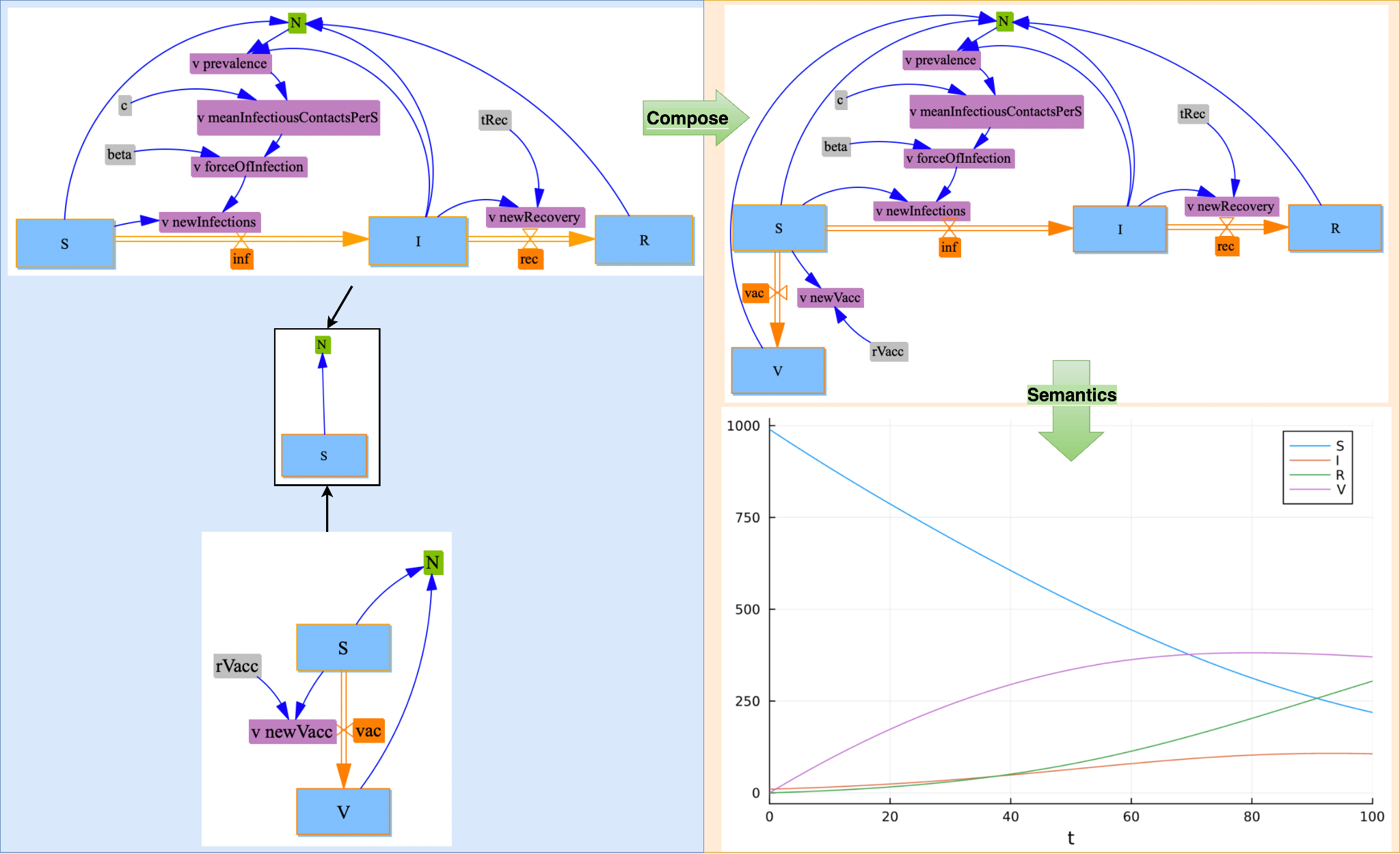
Categorical views of compositional modeling.

b. Open-source software ecosystem

To make these ideas tangible, my group develops open-source software within the AlgebraicJulia ecosystem, creating next-generation dynamic modeling tools—particularly for public health applications.
These platforms aim to make model construction reusable, auditable, and collaborative across mathematics, computer science, and domain sciences.

🎓 Ideal Student Profile

Students with backgrounds in pure mathematics, theoretical computer science, or mathematical logic are well-suited.
Curiosity about category theory and enthusiasm for connecting abstract ideas with computational tools are especially valued.

2️⃣ 🚀 Application-Driven Line — Dynamic Modeling for Real-World Decision-Making

This line focuses on computational dynamic modeling methodologies, Bayesian machine learning algorithms, and large-scale observational data to simulate real-world problems and support better decision-making in public health.
We combine mechanistic insight with statistical learning to understand how behavior, policy, and disease dynamics co-evolve over time.

a. Bayesian ML for data-informed decision support

We develop Bayesian dynamic models—including Particle Filtering, MCMC, Particle MCMC, and Kalman Filtering—that integrate observational data with mechanistic structure.
These models enable probabilistic reasoning while using dynamic systems to transparently represent the underlying structures of real-world problems.
Observed data often provide only partial views of these systems; therefore, we apply Bayesian machine learning algorithms to infer and reconstruct the hidden dynamics, revealing and resolving the full complexity of the system in a transparent way.

b. Modeling complex adaptive systems

We combine System Dynamics for population-level flows, Agent-Based Modeling for individual behaviors, and Discrete-Event Modeling for event-driven processes into hybrid architectures that capture multiple scales of interaction.
Such models allow us to simulate epidemics, evaluate interventions, and design more resilient public health strategies.

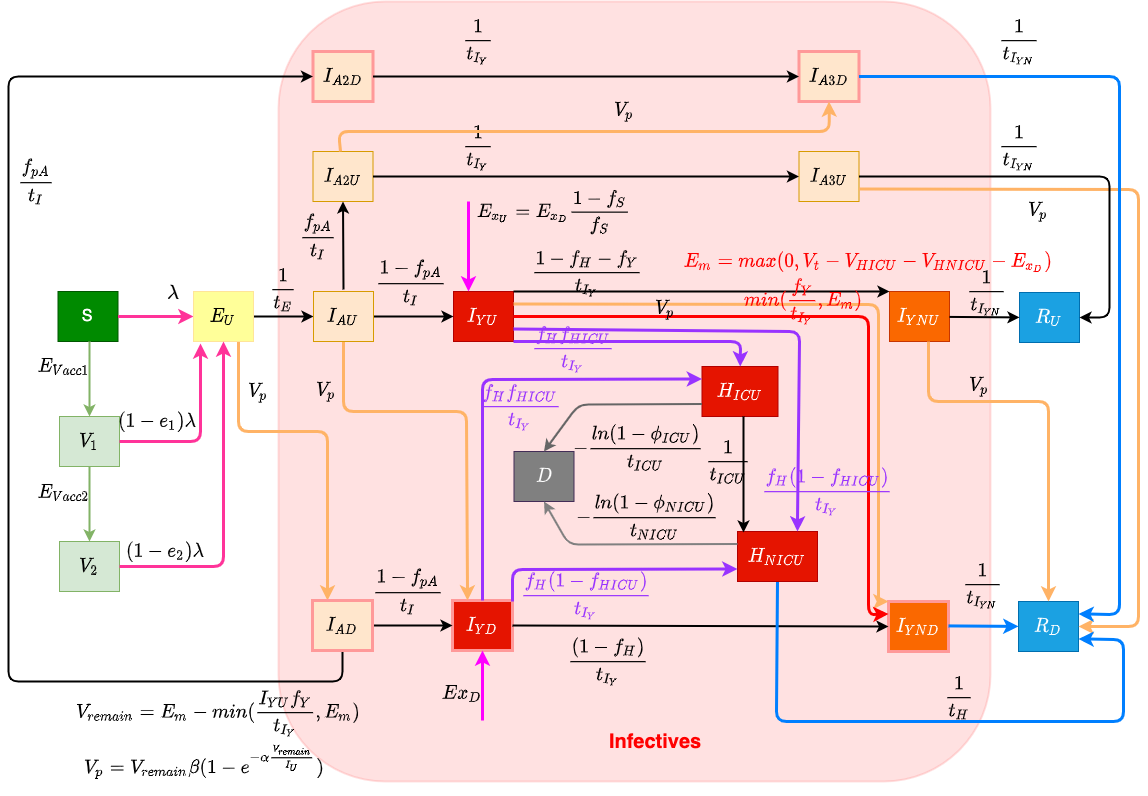
Data-informed and hybrid dynamic modeling for public-health applications.

🎓 Ideal Student Profile

Students with training in applied mathematics, statistics, machine learning, or computational modeling are encouraged to join.
Those excited by real-world applications—from epidemiological forecasting to behavioral interventions—will find many opportunities to contribute.

🌐 Integration and Vision

The two research lines are mutually reinforcing:
the theoretical frameworks provide mathematical coherence and composability, while the applications reveal new structural and computational challenges that shape the theory.
Together they advance a unified vision of compositional, Bayesian, and data-driven modeling—a language for understanding and steering complex adaptive systems.